Innsjømodellering
Beregningene utført av applikasjonen, og beskrevet på denne siden, er en delmengde av de som er tilgjengelig i den originale TPKALK-applikasjonen. Utviklet av NIVA i løpet av 1990-tallet.
1 Bakgrunn
1.1 Kalkingsmaterialer
Kalkprodukter som brukes til nedbørfeltforvaltning er vanligvis en blanding av kalsiumkarbonat (kalsitt, \(CaCO_3\)) og magnesiumkarbonat (\(MgCO_3\)). Bergarter som hovedsakelig består av \(CaCO_3\) kalles vanligvis kalksteiner og kritt, mens karbonatbergarter med betydelige andeler magnesium kalles dolomitter (> 10% Mg), eller magnesianske kalksteiner (2 til 10% Mg).
Kalkprodusenter vil typisk spesifisere andelen kalsium- og magnesiumkarbonat i produktene sine. For eksempel er ‘Microdol5’ rapportert å være 53,7% \(CaCO_3\) og 44,4% \(MgCO_3\) etter masse (med 1,9% andre urenheter).
Magnesiumkarbonat har en høyere andel karbonat etter masse og derfor en større syrenøytraliserende kapasitet (“Acid Neutralising Capacity”; ANC) enn kalsiumkarbonat: 1 g magnesiumkarbonat vil nøytralisere like mye syre som 1,19 g kalsiumkarbonat. Når man sammenligner kalk med forskjellige sammensetninger, er det derfor nødvendig å multiplisere magnesiumkarbonatandelen med en faktor på 1,19. Dette gir en nøytraliserende verdi (NV), beregnet som summen av kalsiumkarbonat ekvivalenter (f.eks. Tabell 1). NV bestemmes best ved titrering i henhold til EN-12945. Det kan også estimeres fra Ca- og Mg-elementanalyser, men i noen tilfeller kan disse elementene være fiksert til andre mineraler enn karbonater med liten eller ingen nøytraliserende kapasitet.
| Produkt | CaCO3 (%) | MgCO3 (%) | MgCO3 (CaCO3-ekv; %) | NV (sum of CaCO3-ekv; %) |
|---|---|---|---|---|
| Microdol5 | 53.7 | 44.4 | 52.8 | 106.5 |
| VK3 | 99.0 | 1.0 | 1.2 | 100.2 |
NV er vanligvis spesifisert i prosent: rent kalsiumkarbonat har en NV på 100%; rent magnesiumkarbonat har en NV på 119%; og typiske dolomittprodukter har NV-er som er et sted i mellom. For samme masse vil produkter med høyere NV være mer effektive til å øke pH, så lenge all kalken løses opp. I praksis viser forskjellige kalker forskjellige oppløsningshastigheter, som også må tas med i betraktningen (Avsnitt 1.2).
1.2 Kalkløselighet
Flere faktorer påvirker oppløsningshastigheten til kalkmateriale som tilsettes en vannmasse. Disse inkluderer:
Fysiske og kjemiske egenskaper til kalkmaterialet (krystallstruktur etc.).
Partikkelstørrelse (dvs. finhet) av kalkmaterialet. Mindre partikler gir større reaksjonsflate og løses derfor raskere opp.
Vann pH. Surere innsjøer reagerer kraftigere med kalken.
Kalkpåføringsmetode (for eksempel fra båt versus fra helikopter).
Mengde tilsatt kalk, vanligvis kalt dosen. Hvis store mengder kalk tilsettes en innsjø på en gang, er den totale effekten på pH mindre enn det som kunne oppnås hvis mindre mengder ble tilsatt mer regelmessig. Dette skyldes at ved høye doser øker pH og kalsiumkonsentrasjon i umiddelbar nærhet av kalkpartiklene, som så synker til bunnen uten å løses effektivt opp. Det er også mer sannsynlig at kalkpartikler vil klumpe seg sammen og synke raskere. Denne effekten kalles overdosering.
De fleste kommersielle kalkprodukter er fine nok til å oppløses effektivt. For en gitt påføringsmetode og innsjø-pH er målet derfor å identifisere hvilket kalkprodukt som skal brukes (dvs. hvilke fysiske og kjemiske egenskaper som skal velges) og i hvilken dose (for å minimere antall påføringer som er nødvendig uten overdosering).
Kalkoppløsningshastigheter og effekten av overdosering bestemmes eksperimentelt - se kolonnetester for detaljer.
2 Modelleringsprosedyre
Målet med modellen er å simulere endringer i innsjøens pH på grunn av kalking med ulike produkter. Det gir en del av bevisgrunnlaget for å avgjøre hvilke kalkprodukter som skal brukes under ulike omstendigheter.
Modellen forsøker å simulere en “typisk” innsjø og resultater må derfor betraktes som illustrative. Målte data fra ekte innsjøer viser at dose-respons-forhold er svært varierende og kan avhenge sterkt av lokale faktorer. Modellen bruker idealiserte empiriske sammenhenger basert på norske overvåkingsdata og laboratorietester. Den er ikke egnet for detaljert simulering av individuelle innsjøer.
2.1 Forholdet mellom Ca-ekvivalenter og pH
Når vi tilsetter kalkingsmateriale, øker konsentrasjonen av CaCO3 (og MgCO3, hvis relevant) i innsjøen, noe som fører til en økning i pH. Figur 1 viser forhold utledet empirisk av Atle Hindar som relaterer endringer i CaCO3-ekvivalenter til endringer i pH for innsjøer med forskjellige konsentrasjoner av totalt organisk karbon (TOC).
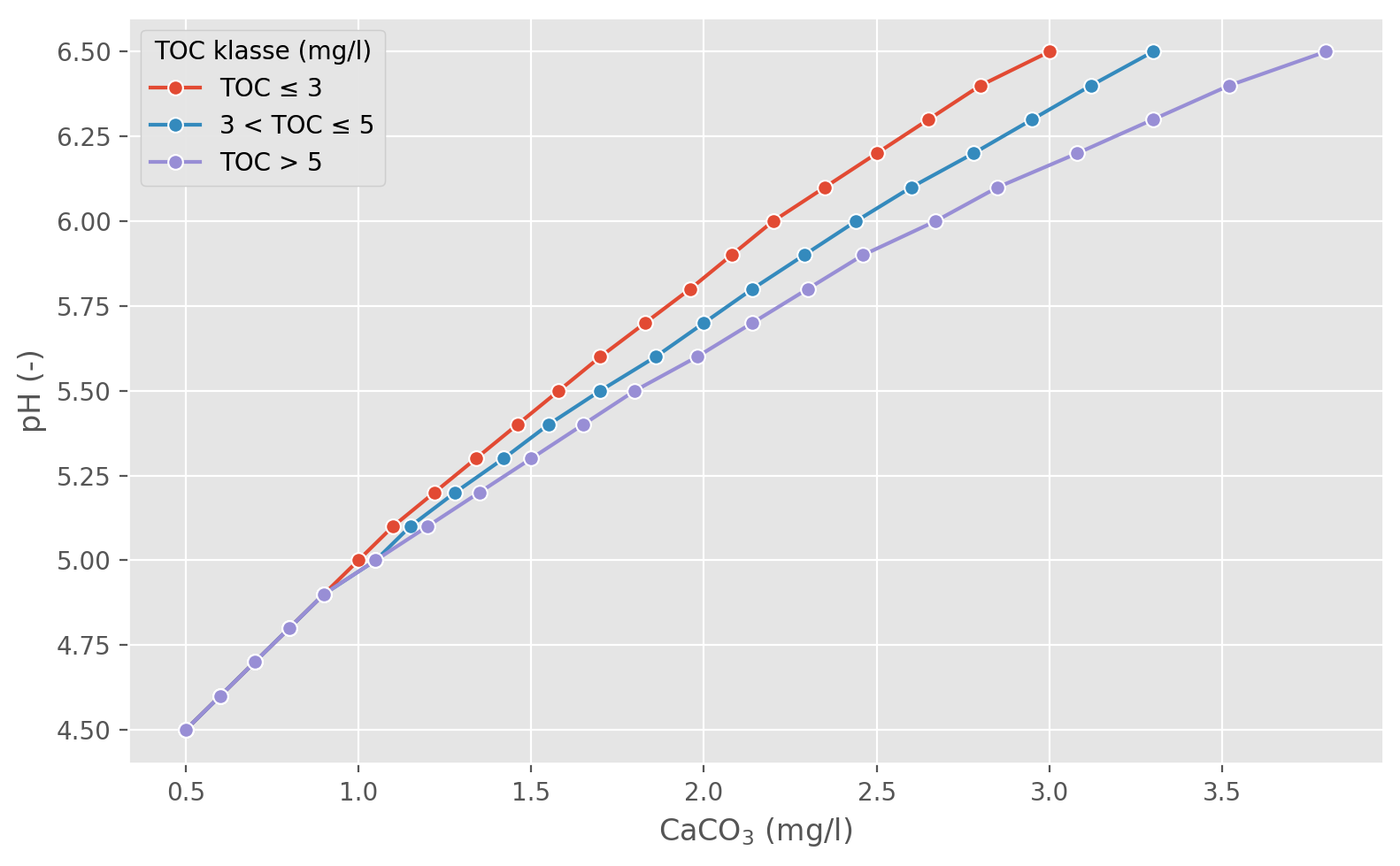
For en innsjø med en gitt initiell pH- og TOC-konsentrasjon, bruker modellen sigmoid-kurver basert på empiriske data (Figur 2) for å finne en idealisert CaCO3-konsentrasjon som representerer innsjøens initielle bufferkapasitet. Modellen simulerer deretter endringer i CaCO3-ekvivalente konsentrasjoner over tid (i forhold til startkonsentrasjonen), og bruker kurvene til å estimere tilsvarende endringer i pH.
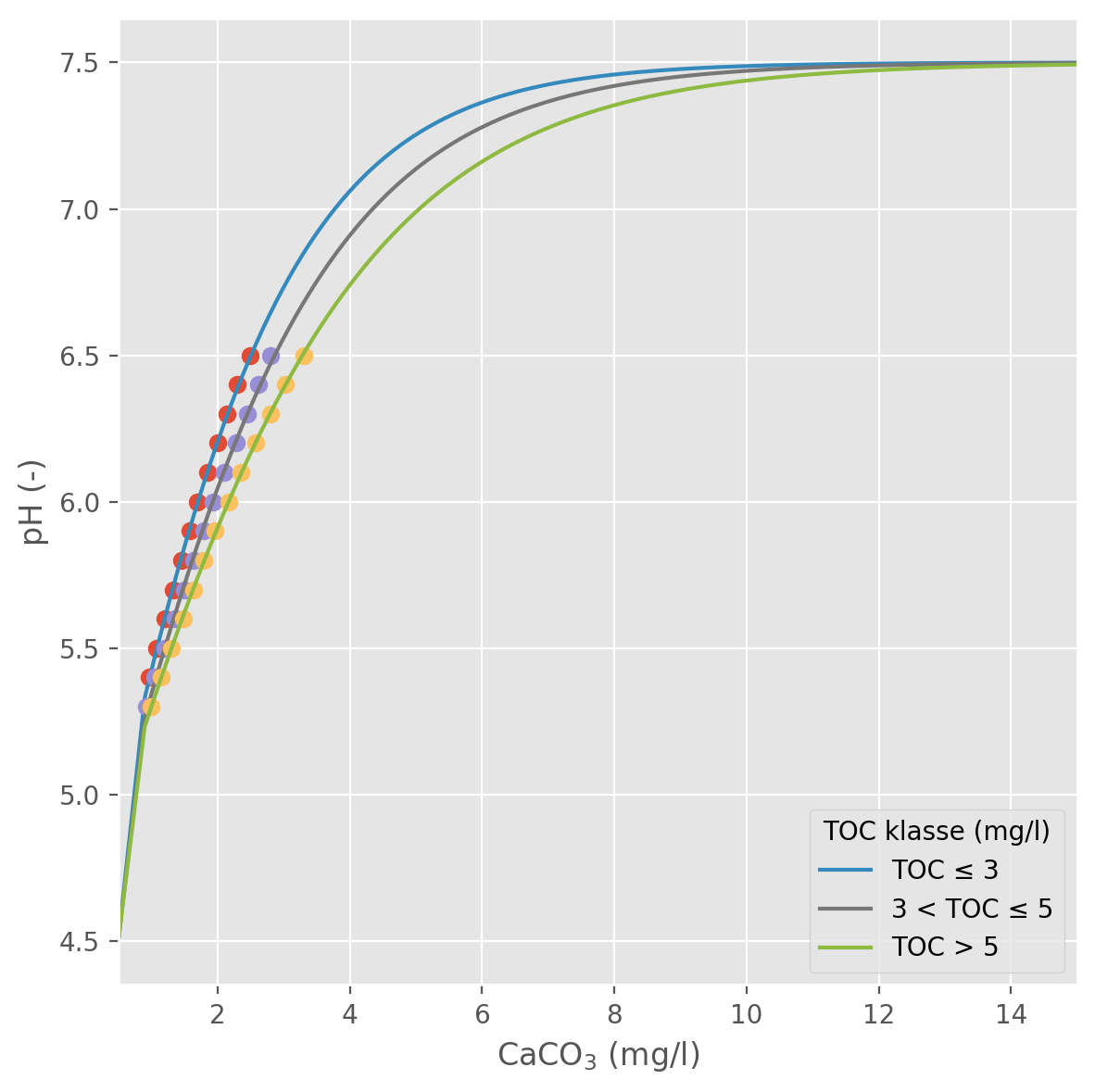
2.2 Massebalansemodell
Titreringskurvene i Figur 2 transformerer problemet med modellering av pH til modellering av \(\Delta Ca\) (og \(\Delta Mg\) også, hvis relevant). Når vi tilsetter kalk til en innsjø, løses noe av den opp umiddelbart, noe som gir en plutselig økning i pH, mens resten synker til bunnen og løses opp langsommere.
En massebalanse “boksmodell” (Figur 3) brukes for å gi et estimat av både den umiddelbare endringen i innsjøforhold på grunn av kalking og den påfølgende utviklingen over tid. For enkelhets skyld vises kun ett sett med beregninger (f.eks. for kalsium), men et identisk sett med beregninger for magnesium utføres også parallelt, hvis det er relevant. Mg-fraksjonen omdannes deretter til CaCO3-ekvivalenter før det knyttes til endringer i pH (Avsnitt 2.1). Med kalsium som eksempel, er symbolene i Figur 3 som følger:
- \(D\) er dosen av tilsatt kalk (justert for Ca-innhold, dvs. den faktiske dosen av Ca i mg/l).
- \(C_{inst}\) er den “umiddelbare” økningen i innsjøens Ca-konsentrasjon (i mg/l) på grunn av momentanoppløsning.
- \(C_{bott} = (D - C_{inst})\) er mengden Ca (i mg/l) som synker til bunnen av innsjøen og oppløses langsommere.
- \(F_{slow}\) er hastigheten som konsentrasjonen øker med (i mg/l/måned) på grunn av oppløsning av bunnlaget.
- \(C_{in}\) og \(C_{out}\) er henholdsvis innløps- og utløpskonsentrasjonene av Ca (begge i mg/l).
- \(V\) er innsjøvolumet i liter. Innsjøen antas å være “stabil”, dvs. \(V\) er konstant.
- \(Q\) er vannføringen i l/måned. For å tilfredsstille den “stabil”-forutsetningen, må innløpsvannføringen være likt utløpsvannføringen.
- \(M_{lake}\) er massen av Ca oppløst i innsjøvannet (i mg).
- \(C_{lake}\) er Ca-konsentrasjonen i innsjøen, lik \(\frac{M_{lake}}{V}\). Innsjøen antas å være godt blandet, slik at utløpskonsentrasjonen, \(C_{out}\), er lik \(C_{lake}\).
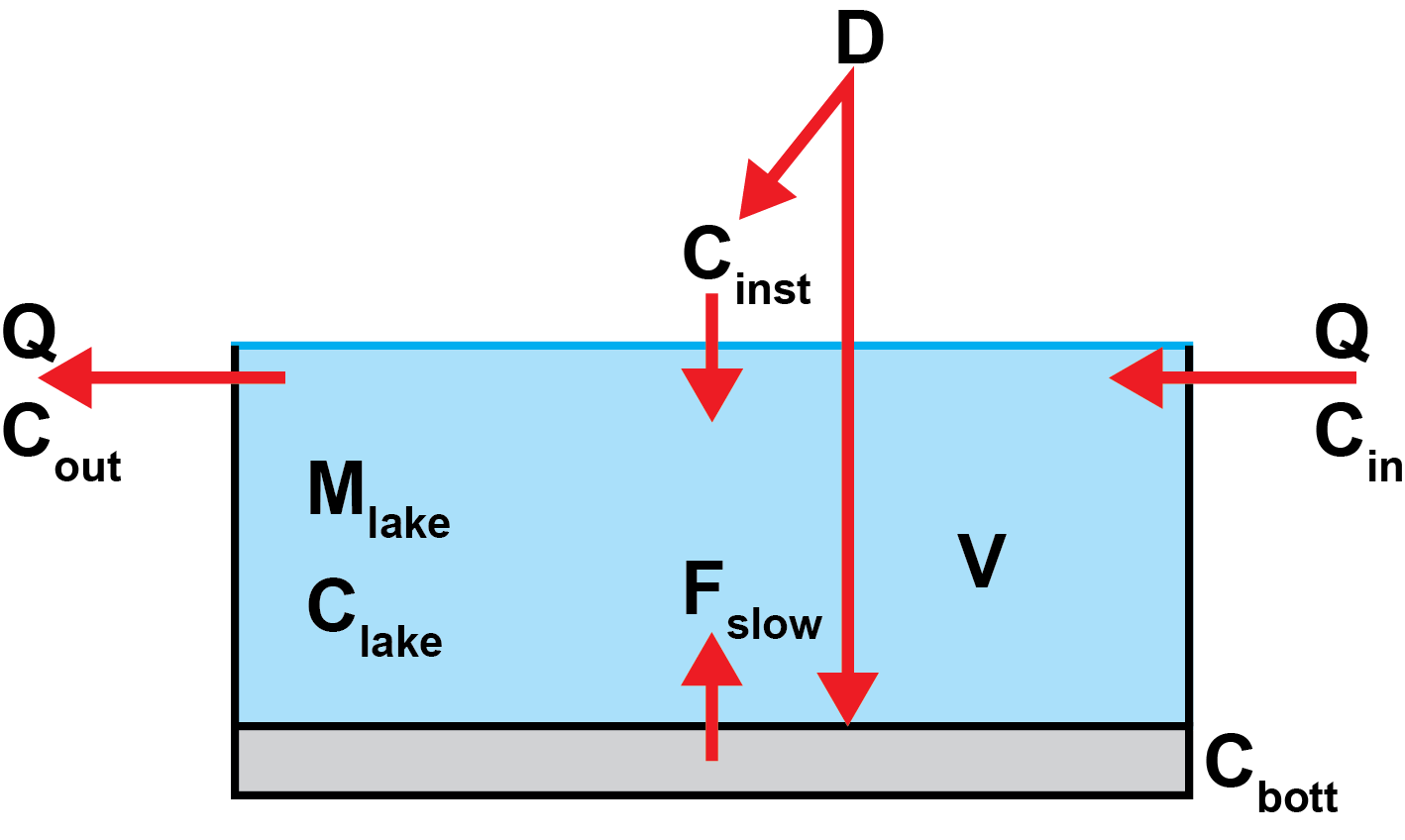
Balansering av de viktigste kildene og synker av Ca til innsjøen gir
\[ \frac{dM_{lake}}{dt} = V \frac{dC_{lake}}{dt} = Q C_{in} - Q C_{lake} + V C_{inst} + V F_{slow} \tag{1}\]
eller
\[ \frac{dC_{lake}}{dt} = \frac{Q C_{in} - Q C_{lake}}{V} + C_{inst} + F_{slow} \tag{2}\]
Kalk som ikke løses opp umiddelbart synker til bunnen av innsjøen og løses opp saktere (\(C_{bott}\)). Oppløsning av innsjøbunnkalk modelleres som en førsteordens reaksjon med starthastighetskoeffisient \(K_0\). Imidlertid antas denne hastighetskoeffisienten å avta eksponentielt over tid, basert på observasjonen at kalk som samler seg i innsjøsedimenter blir mindre “aktiv” over tid og derfor oppløses langsommere. Hastigheten som reaksjonskoeffisienten avtar med styres av “aktivitetskoeffisienten”, \(\lambda\)
\[ K_t = K_0 e^{- \lambda t} \tag{3}\]
der \(K_t\) er førsteordens reaksjonskoeffisient ved tidspunktet \(t\).
Den effektive hastighetskoeffisienten, \(K_t\), modifiseres ytterligere av en faktor, \(R\), som reduserer oppløsningshastigheten ettersom konsentrasjonene av oppløst CaCO3 i innsjøen blir høye. Spesielt tvinger \(R\) \(K_t\) mot null når oppløste konsentrasjoner nærmer seg metning. Dette gjøres først og fremst for å sikre at modellens resultater forblir plausible selv om brukere setter ekstreme parameterverdier i brukergrensesnittet; for de fleste realistiske valg av modellparametere vil ikke innsjøkonsentrasjoner nærme seg metning og verdien av \(R\) vil være nær 1.
\[ R = \frac{1}{1 + e^{10 (C_{lake} - C_{sat})}} \tag{4}\]
der \(C_{sat}\) er metningskonsentrasjonen av Ca i innsjøvann (dvs. den maksimale verdien tillatt av modellen).
\[ F_{slow} = - \frac{dC_{bott}}{dt} = C_{bott} K_t R \tag{5}\]
2.3 Momentanoppløsning
For at modellen skal produsere fornuftige simuleringer, er det viktig å ha et nøyaktig estimat for andelen kalkmateriale som løses opp raskt (dvs. den momentanoppløsningsfraksjonen, \(C_{inst}\)). Momentanoppløsning kan måles i laboratoriet ved hjelp av kolonnetester, som forteller oss hvor mye kalk som typisk vil løses opp i en kolonne gitt en kjent initiell pH og kalkdose. Før kolonnetestdataene kan brukes til innsjømodellering, er det nødvendig å justere for:
Spredningsmetode. For tørrspredning (f.eks. med helikopter) er mengden kalkmateriale som oppløses umiddelbart typisk 0,5 til 0,7 ganger andelen forutsagt av kolonnetester. Ingen justering er nødvendig for våtspredning (f.eks. fra båt).
Innsjødybde. Dypere innsjøer gir kalken mer tid til å løse seg opp når den synker. I sin doktorgradsavhandling bemerket Sverdrup (1985) at for CaCO3 er den momentanoppløsningen direkte proporsjonal med både \(H^+\) konsentrasjon og synking dybde
\[ D_{inst} \propto [H^+] \times d \tag{6}\]
Det er derfor mulig å generalisere momentanoppløsningsestimater fra kolonnetester med fast dybde til innsjøer med forskjellige dybder ved å vurdere kompenserende endringer i pH. For eksempel er forventet oppløsning for en innsjø med dybde \(d\) og hydrogenionkonsentrasjon \(H^+\) den samme som for en innsjø med dybde \(2d\) og hydrogenionkonsentrasjon \(0,5H^+\). For konvertering til pH, antas momentanoppløsningen for en innsjø med dybde \(d_{lake}\) og initiell pH \(X\), å være lik oppløsningen i en testkolonne med dybde \(d_{col}\) og pH \((X - a)\). Der \(a\) er gitt av:
\[ a = log(\frac{d_{lake}}{d_{col}}) \tag{7}\]
Merk at Ligning 7 gjelder for CaCO3-fraksjonen; for MgCO3 foreslo Sverdrup modifikasjonen \((X - 0,5a)\) som en mer passende dybdekorreksjon.
2.4 Simulering av en “standard innsjø”
Modellen definert ovenfor er i stand til å simulere hvordan pH og Ca-konsentrasjon (og Mg, hvis relevant) endres over tid for en enkelt innsjø. Modellen krever følgende inndata:
Innsjø volum (ofte oppgitt som overflateareal og gjennomsnittlig dybde) og vannføring, som sammen definerer oppholdstiden. Merk at denne modellen forutsetter at volumet er fast, men vannføringen kan variere over tid, om ønskelig.
Innsjøens pH, innløps-pH og TOC-konsentrasjon.
dosen av tilsatt kalkmateriale og andelen Ca og Mg etter masse i kalken. Overdoseringsfaktorer er også relevante for høyere doser.
Innsjømiddeldybde og spredningsmetode (dvs. “våt” eller “tørr”), som begge brukes til å justere de momentanoppløsningsverdiene fra kolonnetester (Ligning 7).
Parameterne \(K_0\) og \(\lambda\), som bestemmer hvor raskt kalk på innsjøbunnen løses opp, og hvor lenge den forblir “aktiv”.
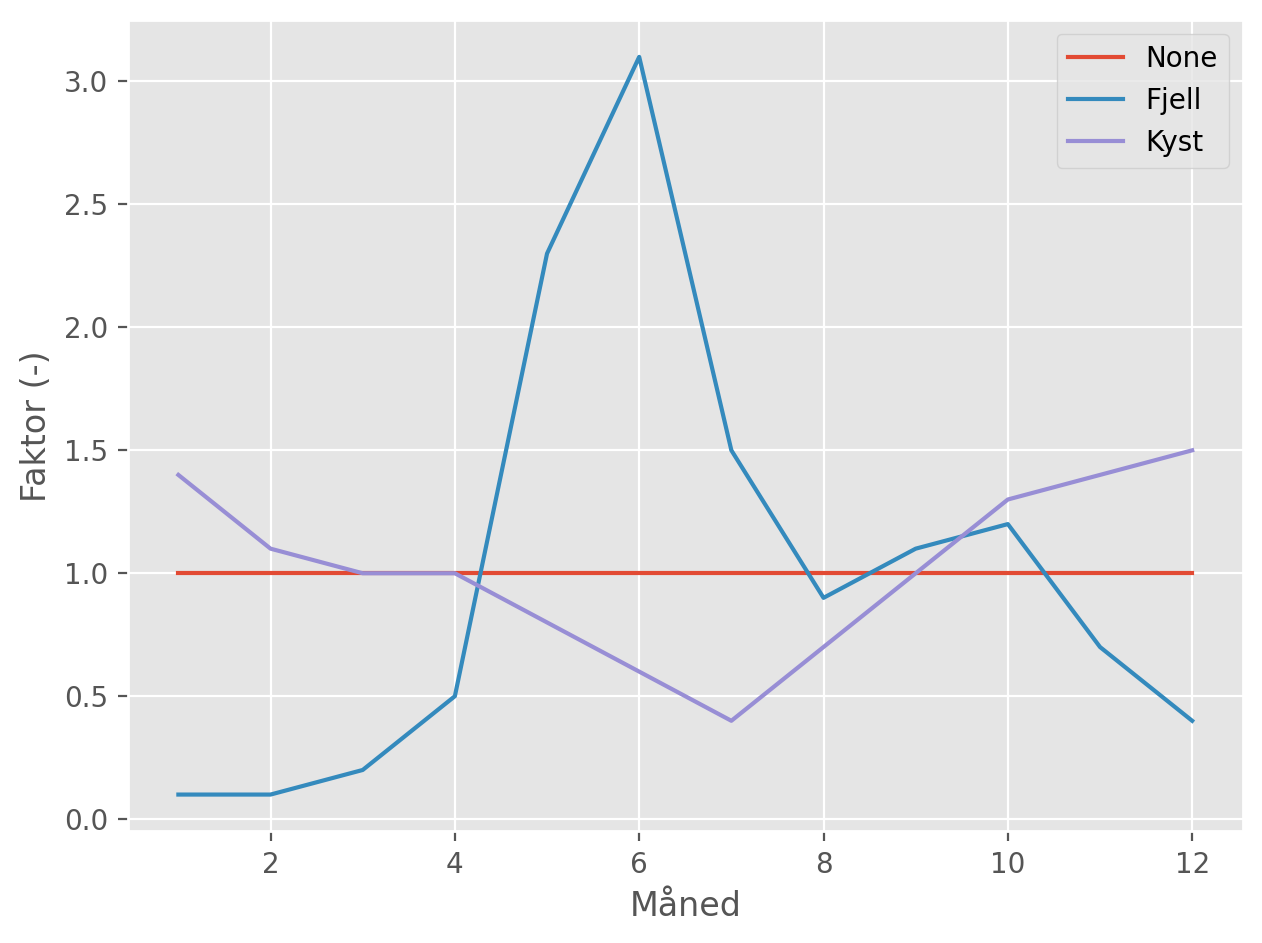
For å unngå å måtte spesifisere alle disse parameterne ved sammenligning av ulike kalkprodukter, er det vanlig å vurdere en standard innsjø med et areal på 20 ha, gjennomsnittlig dybde på 5 m og gjennomsnittlig oppholdstid på 0,7 år. Disse parameterne definerer i sin tur gjennomsnittlig årlig utslipp. Om ønskelig kan dette endres ved å velge en månedlig vannføringsprofil (fjell eller kyst; se Figur 4), som justerer vannføring opp eller ned i hver måned, men på en slik måte at det samlede årlige gjennomsnittet opprettholder en oppholdstid på 0,7 år.