Kolonnetester
Når kalk tilsettes en innsjø, løses noe raskt opp mens resten synker til bunnen hvor det løses opp saktere. Hvor mye av kalken som umiddelbart løses opp avhenger av innsjøens kjemi, påføringsmetoden og egenskapene til kalkproduktet som brukes (se Innsjømodellering for detaljer).
Andelen av et kalkprodukt som vil løse seg opp “umiddelbart” kan estimeres ved hjelp av kolonnetester (i dette tilfellet betyr begrepet “umiddelbart” “innen dager”, i stedet for uker, måneder eller år). Hvert eksperiment involverer 5 kolonner, merket “A” til “E”. Kolonnene er 19 cm i diameter og minst 205 cm høye, og de fylles i utgangspunktet med 57,9 liter avionisert vann inneholdende 0,01 % KCl, justert til ønsket pH ved bruk av svovelsyre.
For hvert kalkprodukt som testes, må leverandøren spesifisere de typiske proporsjonene av Ca og Mg (i masse) i produktet, \(F_{Ca}\) og \(F_{Mg}\). Disse er brukt i beregningene nedenfor.
1 Momentanoppløsning
For hver type kalk vil vi gjerne vite hvor stor andel som løses opp “umiddelbart” for en rekke initielle pH-verdier og dosekonsentrasjoner. Dosen uttrykkes vanligvis som en konsentrasjon i mg/l kalk, dvs. totalt tilsatt kalkmasse, delt på totalt volum av vann i kolonnen (eller innsjøen). Hvis dosekonsentrasjonen er \(D \ mg/l\) kalk og andelen kalsium i kalkproduktet pr. masse er \(F_{Ca}\), vil konsentrasjonen av Ca i kolonnen være \(F_{Ca} D \ mg/l\), dersom all kalken løses helt opp. Målet med testene er å se hvor mye av kalken som faktisk løses opp under ulike forhold.
1.1 Endring av pH
For det første settet med tester blir kolonnene “A” til “E” justert til å ha pH-verdier på henholdsvis 4, 4,5, 5, 5,5 og 6. Deretter tilsettes 0,579 g tørket kalk i toppen av hver kolonne, tilsvarende en jevn dose på 10 mg/l kalk. Hvis alt dette løses opp og blandes jevnt, er den totale massen av Ca eller Mg oppløst i kolonnen mellom to dybder \(x_1\) og \(x_2\) (der \(x_2 > x_1\)) gitt av:
\[ M_{par} = 10 F_{par} A (x_2 - x_1) \tag{1}\]
\(A\) er tverrsnittsarealet til kolonnen og \(par\) er enten Ca eller Mg.
I praksis løser ikke all kalken seg opp og kolonnene oppnår ikke jevne konsentrasjoner. Etter 16 timer måles konsentrasjonen av Ca (og Mg, hvis relevant) i hver kolonne ved forskjellige dybder ved bruk av ICP-OES (Inductively Coupled Plasma - Optical Emission Spectrometry). Fem konsentrasjoner er tatt fra hver kolonne med 40 cm intervall fra overflaten ned til 1,6 m. Et typisk datasett for en enkelt kolonne for en ikke-dolomittisk kalk (dvs. bare Ca) er vist i Tabell 1.
| Kolonne | pH | Dybde (m) | Ca (mg/l) |
|---|---|---|---|
| A | 4.0 | 0.0 | 2.82 |
| A | 4.0 | 0.4 | 2.62 |
| A | 4.0 | 0.8 | 2.64 |
| A | 4.0 | 1.2 | 2.76 |
| A | 4.0 | 1.6 | 2.81 |
Tabell 1 brukes til å estimere den totale mengden Ca som faktisk har løst seg opp i hver kolonne etter 16 timer. Det antas at hver kolonne er horisontalt godt blandet og at konsentrasjonene kun varierer med dybden, \(x\). Den totale mengden Ca mellom dybdene \(x_1\) og \(x_2\) er gitt av integralet:
\[ M_{Ca} = A \int_{x_1}^{x_2} C(x) \ dx \tag{2}\]
Den totale andelen av tilgjengelig Ca som har løst seg opp, kalt momentanoppløsning, kan deretter beregnes ved å dele Ligning 2 med Ligning 1, begge evaluert mellom 0 og 1,6 m dybde (og samme beregning utført for magnesium, hvis relevant).
\[ D_{inst} = \frac{\int_{0}^{1.6} C(x) \ dx}{10 F_{Ca} (1.6 - 0)} \tag{3}\]
Integralet i Ligning 3 er tilnærmet fra de målte dataene (Tabell 1) ved å bruke trapesregelen.
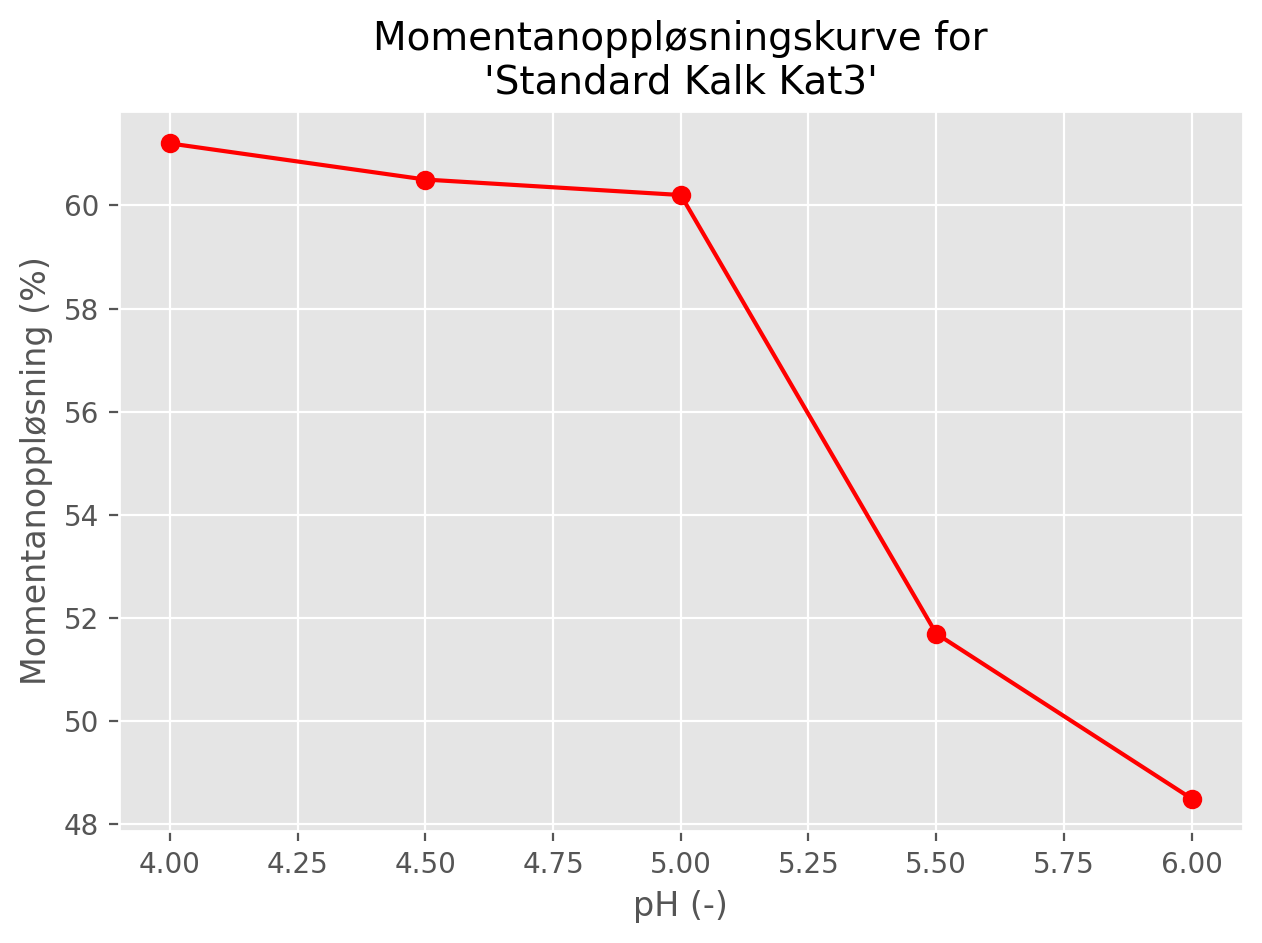
Hovedresultatet fra dette eksperimentet er et sett med momentanoppløsningsverdier (vanligvis uttrykt i prosent) som viser hvordan oppløsningen endres med initiell pH ved en fast kalkdose (Figur 1).
1.2 Endring av dose
I den andre testen fikseres kolonnene “A” til “E” til pH 4,5 og ulike doser tilsettes hver kolonne, tilsvarende kalkkonsentrasjoner på 10, 20, 35, 50 og 85 mg/l (forutsatt fullstendig oppløsning). Kolonnene får igjen stå i 16 timer og momentanoppløsningen for hver kolonne bestemmes ved å bruke prosedyren beskrevet i Avsnitt 1.1.
Ved høye doser er andelen kalk som løser seg umiddelbart typisk lavere enn i den første testen, fordi høye doser fører til høye kalsiumkonsentrasjoner nær kalkpartiklene, noe som hemmer oppløsning. Denne effekten kalles overdosering.
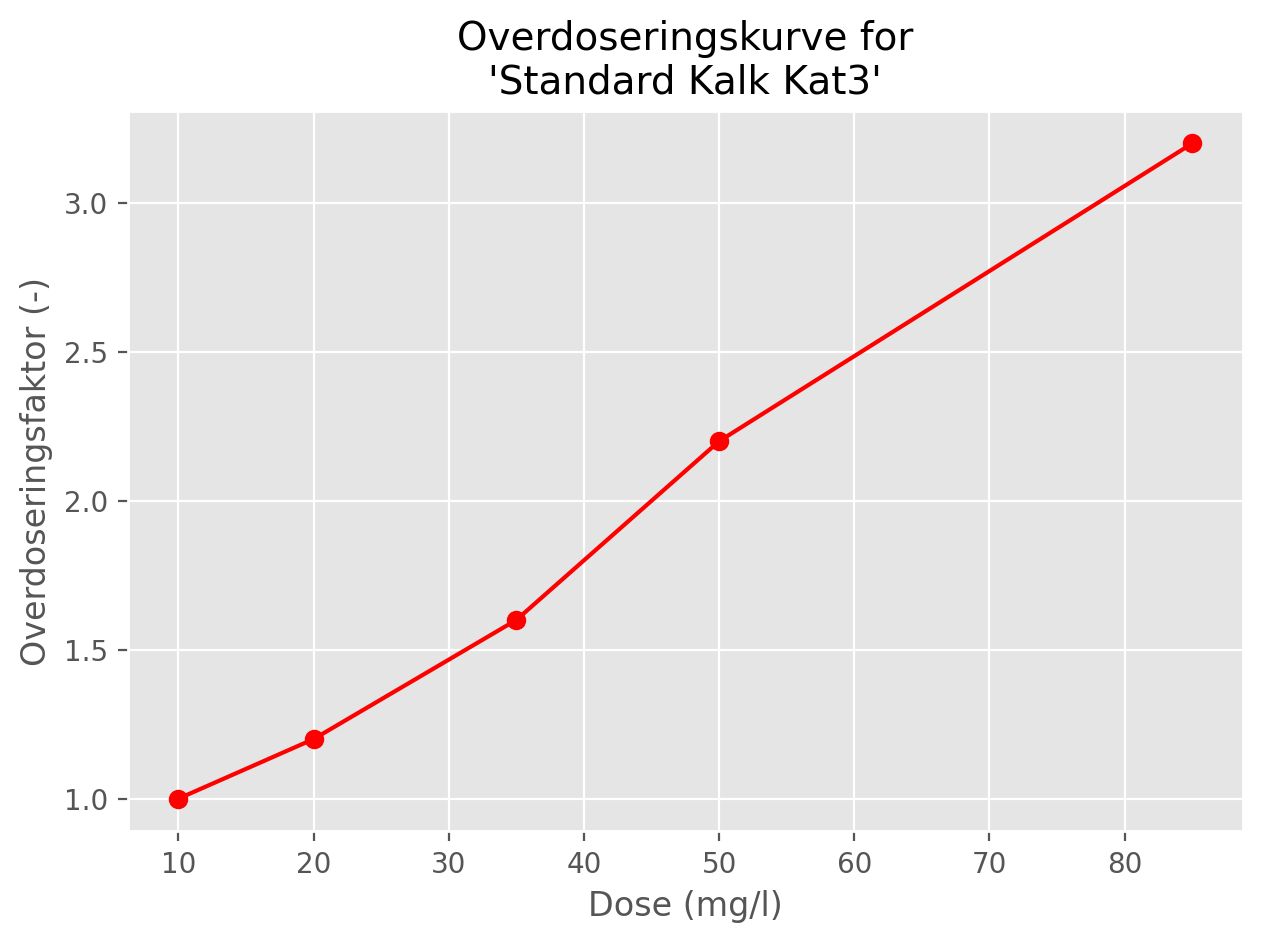
Hovedresultatet fra den andre testen er et sett med overdoseringsfaktorer, beregnet som forholdet \(D_{10} / D_{x}\), der \(D_{10}\) er den momentanoppløsningen for kolonnen der 10 mg/l kalk ble først tilsatt, og \(D_{x}\) er den momentanoppløsningen for kolonnen hvor \(x\) mg/l kalk ble tilsatt.
En typisk kurve for overdoseringsfaktorer er vist i Figur 2.
1.3 Kombinere datasett
De to eksperimentene beskrevet i Avsnitt 1.1 og Avsnitt 1.2 gir data i formatet vist i Tabell 2.
| pH Dose |
4 | 4.5 | 5 | 5.5 | 6 |
|---|---|---|---|---|---|
| 10 | x | x | x | x | x |
| 20 | x | ||||
| 35 | x | ||||
| 50 | x | ||||
| 85 | x |
Ved å bruke disse dataene kan den forventede momentanoppløsningen for enhver pH- og kalkdose estimeres ved interpolering.